浮点数在计算机中二进制表示
- 2019-03-08 22:00:00
- 赵勤松 原创
- 3085
目前的计算机系统,都支持IEEE754,其定义了单精度和双精度浮点数的表示标准
1.单精度浮点数
2.双精度浮点数
其中的s,占了一位,为0表示正,为1表示负,决定了浮点数的正负
exp,在单精度中占8位,在双精度中占11位,决定了浮点数的指数位移,这个在之后详细说明
frac,在单精度中占23位,在双精度中占52位,决定了浮点数的有效数值
下面举例说明一个浮点数,是怎样表示为一个符合IEEE754标准的二进制数值的。
以数值38.38为例,我们分别对整数部分和小数部分进行转换
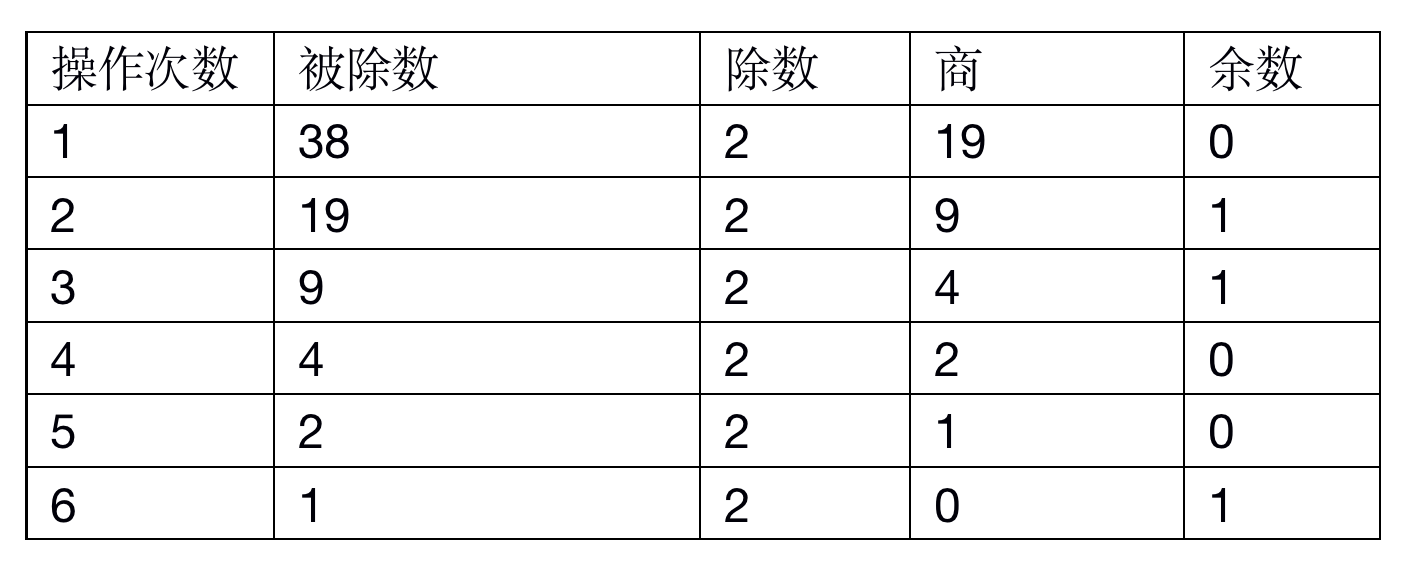
1.整数部分按照除2法进行转换,即将当前整数不断除2,将所得的余数进行逆序排列即可
因此,整数部分的二进制表示为100110.
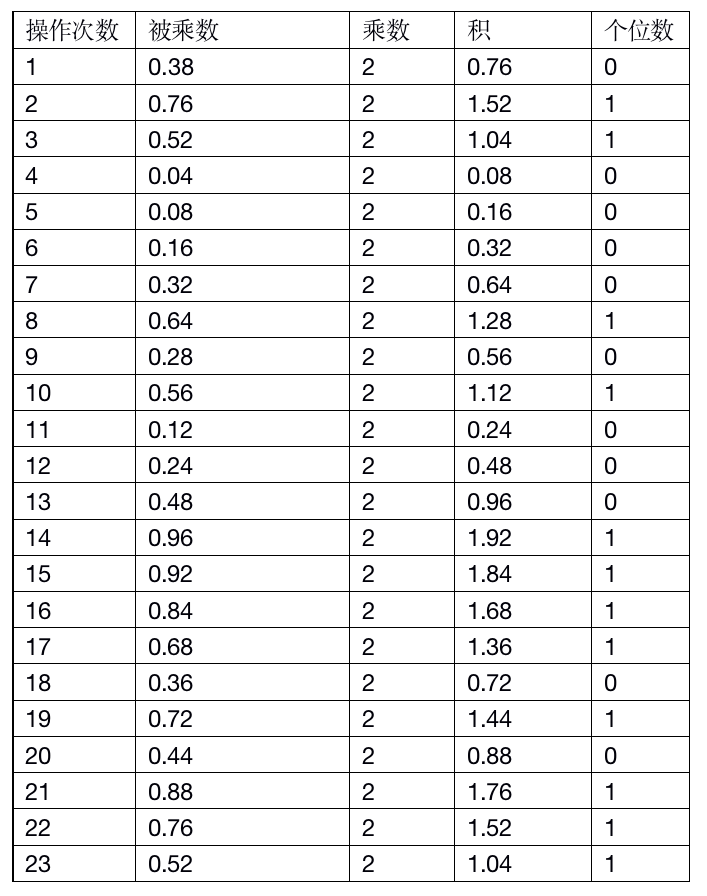
2.小数部分按照乘2法进行转换,即将当前小数乘以2,将所得乘积的个位数进行顺序排列即可(下次运算时取乘积的小数部分)
因此 ,小数部分的二进制可表示为01100001010001111010111.
由此可以将浮点数38.38表示为 100110. 01100001010001111010111.
3.将浮点数进行移位,获得1.xxx这样形式的数值,38.38需要向左移5位,即可表示为 1.00110 01100001010001111010111,这样所有的浮点数都可以统一为整数部分为1的二进制数,因为默认个位数为1,所以只需要将小数部分视为浮点数的有效数值(需要去掉后5位,只需要23位),即frac
4.相信大家可以看出来了,exp部分就是用来记录移位数据的,考虑到我们需要表示很小的数值,exp的最高位为0,其他位为1时,表示不需要移位,以单精度浮点数来说,exp=01111111=127,也就是说,如果exp=127,表示的浮点数为1.xxxx,如果是128,则为1x.xxx,如果是126,则为0.1xxxx,因此我们可以获得,38.38的exp数为127+5=132=10000100.
综上所述,38.38这个浮点数,s=0,exp=10000100,frac= 00110 011000010100011110),所以其二进制数,可完整表示为
01000010000110011000010100011110.
另外,还有一些数,是需要特别规定的.
当exp全为0,frac全为0时,表示0.
当exp全为0,frac不全为0时,表示非标准化值,此时的前导数不为1,而是0,因此可以表示更小的数值.
当exp全为1,frac全为0时,表示无穷大,s=0表示正无穷大,s=1表示负无穷大.
当exp全为1,frac不全为0时,表示NaN,不是合法实数或未初始化.
| 联系人: | powereye |
|---|---|
| Email: | zqs@someapp.cn |
| QQ: | 1134846 |
| 微信: | powereye |